弹性椭圆壳体
弹性椭圆壳体的流固耦合模拟常用来检验浸没边界法的收敛性。 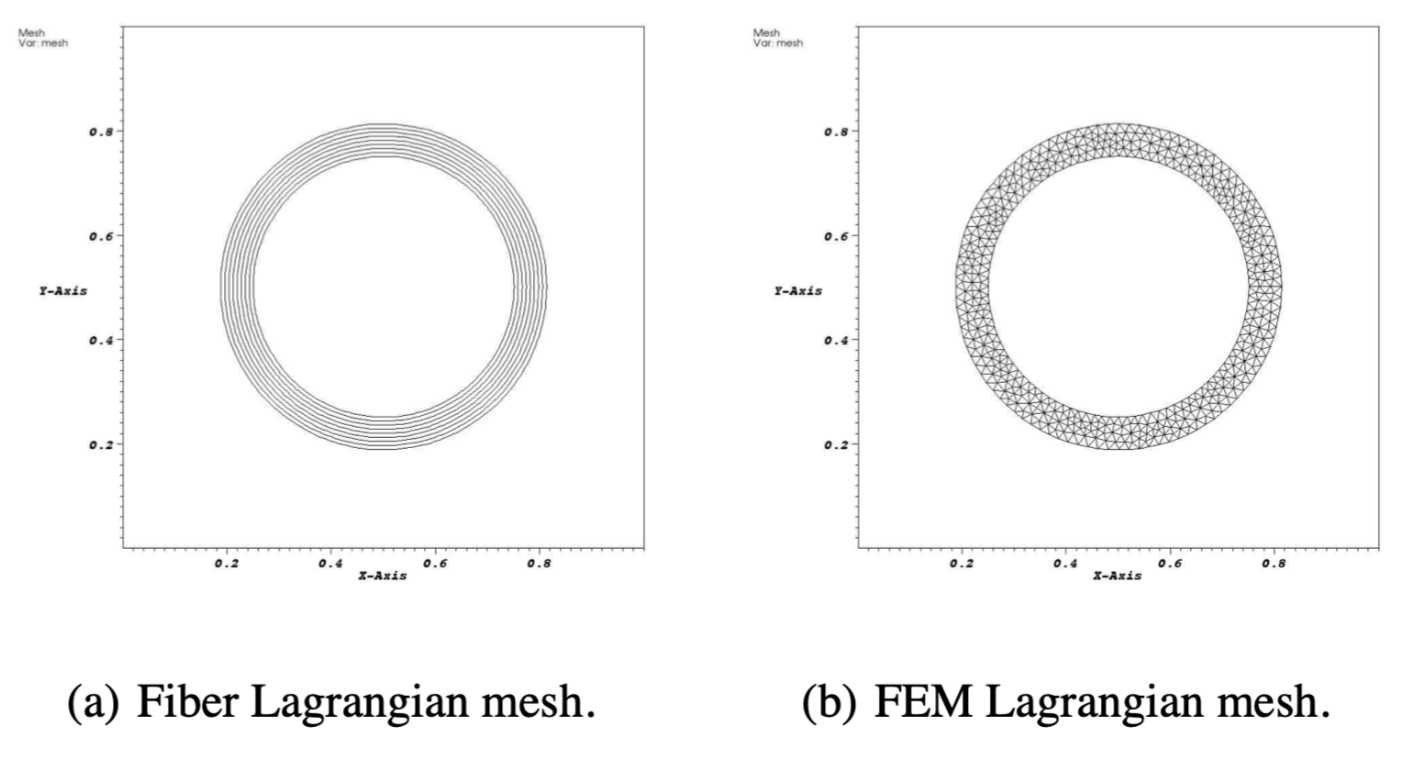
正交异性1壳体
本节使用有限厚度弹性壳体测试收敛性问题。
计算区域为 \(\Omega=[0,1]\times[0,1]\) ,周期边界条件2。
初始的固体区域用曲线坐标描述,
\[ \chi(\textbf{s},0)=\left(\;\;\begin{array}{ll} \text{cos}(s_{1}/R)(R+s_{2})+0.5 \\ \text{sin}(s_{1}/R)(R+\gamma+s_{2})+0.5 \end{array}\;\;\right) \]
其中, \(\textbf{s}=(s_{1},s_{2})\in U=[0,2\pi R]\times[0,\omega]\),沿着\(s_1\)方向的周期边界条件,\(R=0.25\)和\(\omega=0.0625\)。当\(\gamma=0\)时,壳体的初始状态为半径为\(R\)和厚度为\(\omega\)的圆环,结构体处于平衡状态。当\(\gamma\neq 0\)时,壳体的初始状态是一个椭圆形环,处于非平衡状态。
在测试中,静态问题使用\(\gamma=0\),动态问题使用\(\gamma=0.15\)。计算区域\(\Omega\)离散为\(N\times N\)的笛卡尔网格,\(\Delta x\) 为网格间距。固体区域\(U\)离散为\(28M\times M\)的四边形网格,\(M=\frac{1}{M_{fac}}\frac{N}{16}\),网格间距约为\(M_{fa c}\Delta x\),有限元空间使用了\(Q{1}\)元3。
这是一个相对简单的基准问题,其中的静态问题是IB方法中极少数存在解析解的测试问题之一。此外,由于某些 \(\mathbb{P}\) 的选择允许IB方法达到更高阶的收敛率,这个基准问题可以验证我们的算法能否达到数值格式的精度。
参考构型中的中的固体力如何计算
理想各项异性材料
由沿着圆周方向的纤维构成。固体区域在s1方向上是周期边界条件,因此在固体边界上始终有\(\mathbb{P}^{\mathrm{e}} \mathbf{N} \equiv 0\),partitioned weak formulations 和 unified weak formulations 的结果相同。应变能函数、第一PK应力张量、内力密度 \(\mathbf{G}\) 4: \[ W^{\mathrm{e}}(\mathbb{F})=\frac{\mu^{\mathrm{e}}}{2 w}\left\|\frac{\partial \chi}{\partial s_1}\right\|^2=\frac{\mu^{\mathrm{e}}}{2 w} \mathbb{F}_{\alpha 1} \mathbb{F}_{\alpha 1} \]
\[ \mathbb{P}^{\mathrm{e}}=\frac{\partial W^{\mathrm{e}}}{\partial \mathbb{F}}=\frac{\mu^{\mathrm{e}}}{w}\left(\begin{array}{cc} \frac{\partial \chi_1}{\partial s_1} & 0 \\ \frac{\partial \chi_2}{\partial s_1} & 0 \end{array}\right)=\frac{\mu^{\mathrm{e}}}{w}\left(\begin{array}{ll} \mathbb{F}_{11} & 0 \\ \mathbb{F}_{21} & 0 \end{array}\right) \]
\[ \mathbf{G}=\frac{\mu}{w} \frac{\partial^2 \chi}{\partial s_1^2}=\frac{\mu}{w} \frac{1+s_2}{R}\left(\begin{array}{c} -\cos \left(s_1 / R\right) \\ -\sin \left(s_1 / R\right) \end{array}\right)=-\frac{\mu}{w} \frac{1+s_2}{R} \mathbf{r} \]
对于\(\gamma=0\)的静态问题,\(p\)的解析解为 \[ p(x, t) = \begin{cases} p_0 + {\frac{\mu^e}{R}} & r \leq R, \\ p_0 + {\frac{\mu^e}{w}\frac{R + w - r}{R}} & R < r \leq R + w, \\ p_0 & r > R + w. \end{cases} \] 其中,\(r=\|\mathbf{x}-(0.5,0.5)\|\), \[ p_0 = \frac{\pi \mu^e}{3w}{\left(R^2-\frac{ (R+w)^3}{R}\right)}, \]


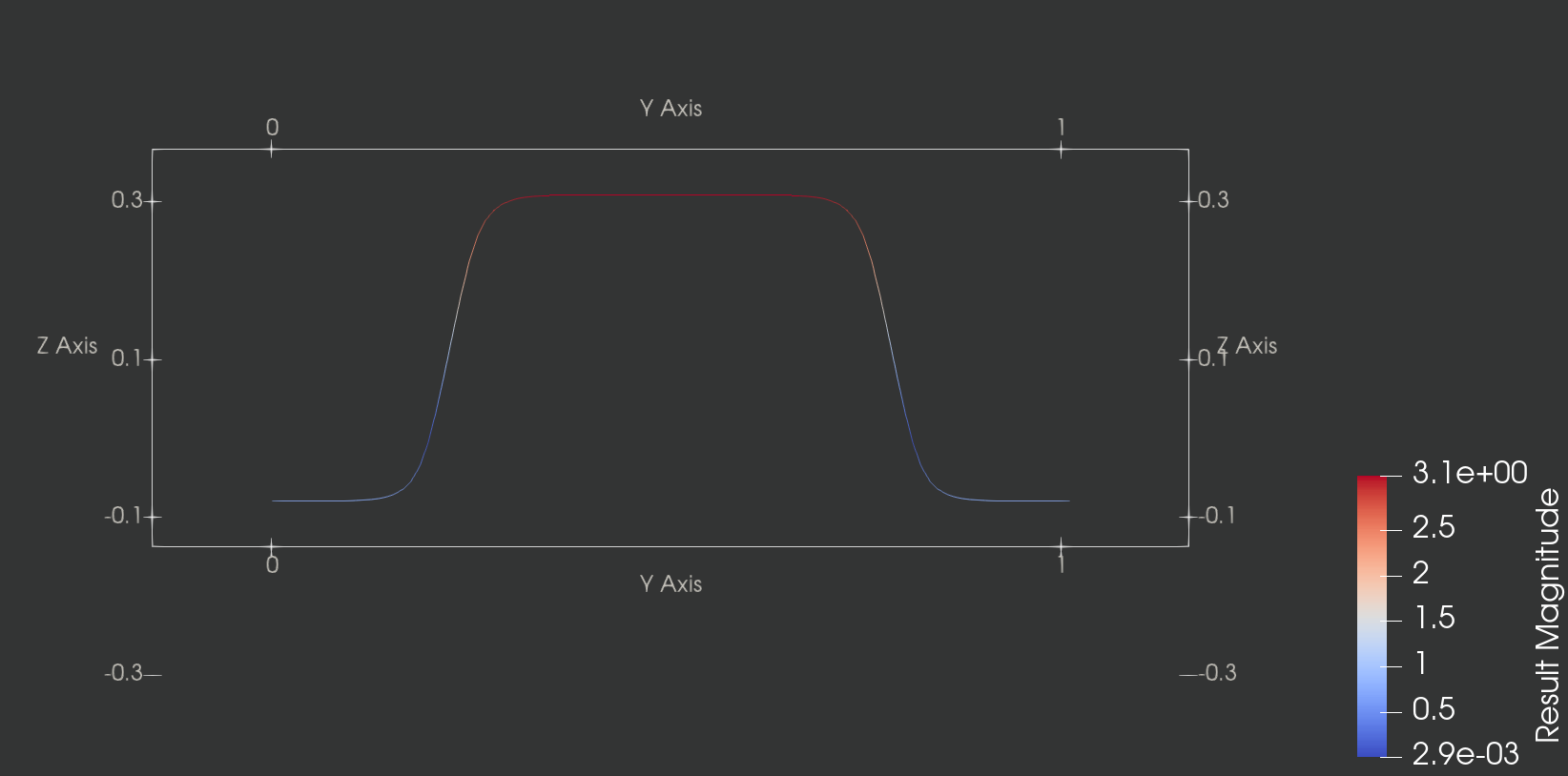

正交异性 Neo-Hookean 材料
由沿着圆周方向和沿着径向的纤维构成,其中沿着径向的纤维在边界处中断,这导致压强和粘性力在界面处是间断的,这也导致了 partitioned formulation 和 unified formulation 的计算结果不同。大部分情况下,两种方法计算出来的位移精度差不多,但是当固体网格较粗时,partitioned formulation 算出压强的结果好一点,能更好地维持体积守恒性。
应变能函数为 \[ W(F)=\frac{\mu^{s}}{2w}I_{1}(\mathbb{C}), \] 其中\(\mathbb{C}=\mathbb{F}^{T}\mathbb{F}\),\(I_{1}(\mathbb{C})=tr(\mathbb{F})\), \[ \mathbb{P}=\frac{\mu^{s}}{w}\mathbb{F}. \] 当\(\gamma=0\)时, 结构体处于平衡状态,施加条件\(\int_{\Omega}p(x,t)dx=0\),可得 $$ p(x,t)=
\[\begin{cases}{l} p_{0}+\mu^{s}(\frac{1}{R}-\frac{1}{R+w}), &r\leq R,\\ p_{0}+\frac{\mu^{s}}{w}(\frac{1}{R}(R+w+r)+\frac{R}{R+w}) &R<r\leq R+w\\ p_{0}&R+w<r. \end{cases}\]$$ 其中\(r=||x-(0.5,0.5)||\)和\(p_{0}=\frac{\pi\mu^{e}}{3w}(3wR+R^{2}-\frac{(R+w)^{3}}{R})\).
画出收敛率折线图
- 总共有五条线,三条为计算结果,两条斜率为1和2的参考线。
- 三条计算结果分别为Mac=1, 2, 4的线。
- 每条线上的节点分别对应背景网格64,128,256,512,1024五个数据。
- 时间步长为0.24*dx。
- 速度分别依L1, L2, L∞ 范数2阶收敛。
- 压强分别依L1, L2, L∞ 范数2阶、1.5阶、1阶收敛。
- 令\(\rho=1,\mu=1,\)和\(\mu^{e}=1\)
令\(\rho=1,\mu=1,\)和\(\mu^{e}=1\),我们考虑时间区间\(0\leq t\leq 3\).图8总结了在时间\(t=3\)时,使用\(M_{fac}=1,2,4\)且\(\Delta t=0.25\Delta x\),\(N=64,128,256,512\)和\(1024\)的误差数据.\(u\)的所有范数都可以观察到一阶收敛性。一阶收敛性也可以通过\(p\)的\(L^{1}\)范数观到。\(p\)在此问题的流固耦合界面上是不连续的。然而当前的方法在\(L^{2}\)范数下产生的收敛速率是0.5和在\(L^{\infty}\)范数下是不收敛的。
我们还考虑了\(\gamma=0.15\),使得壳在初始坐标下是不平衡的。我们设\(\mu=0.01\),\(\rho=1\),且\(\mu^{e}=1\),产生了大约为100的雷诺数。我们考虑的时间区间大约是\(0\leq t\leq 1.25\),其关于壳大约是一个阻尼振动。同样没有一个精确解,因此收敛率使用Richardson 插值估计。图9 总结了当\(N=64,128,256,\)和\(512\)且\(M_{fac}=1\)和\(4\)且\(\Delta t =0.25\Delta x,\)\(t=0.75s\)的误差数据。对于\(u\)和\(\chi\)的所有范数都可以观察到一节收敛率,然而\(p\)只在\(L^{1}\)范数下可观察到一阶收敛率。
对于这个问题我们观察到统一的和分离的公式对于\(u\)和\(\chi\)产生相似的精确解。