SAV 方法求解流固耦合问题(一)
从理论上分析,SAV技术的引入可显著增强IB方法的稳定性,。然而,唯有最终的数值分析结果,才能作为最具说服力的证据。本次数值实验均在IB-FEniCS(暂未开源)中验证。
(Lin et al., 2019)
(Li and Shen, 2020)
(Li and Shen, 2020) 方法需要满足一定的边界条件,以下是我给出的算例。
SAV方法求解NS方程
主要的参考文献有两篇1\(^,\)2,验证稳定性的算例有两个,一个是 Kovasznay 流,另一个是圆柱绕流。
Kovasznay 流
Kovasznay 流的解析解为
其中,\(\lambda=\frac{1}{2 \nu}-\sqrt{\frac{1}{4 \nu^2}+4 \pi^2}\),\(\nu = 0.025\),计算区域为\([-0.5,1.0]\times[-0.5,0.5]\)。这是一个通过非稳态方程求解的稳态问题,给定初值\(\mathbf{u}_0=\mathbf{0}\),源项\(\mathbf{f}=\mathbf{0}\),速度的 Dirichlet 边界条件由解析解给定。如图所示,解析解可以表示一块挡板后面的流体运动。
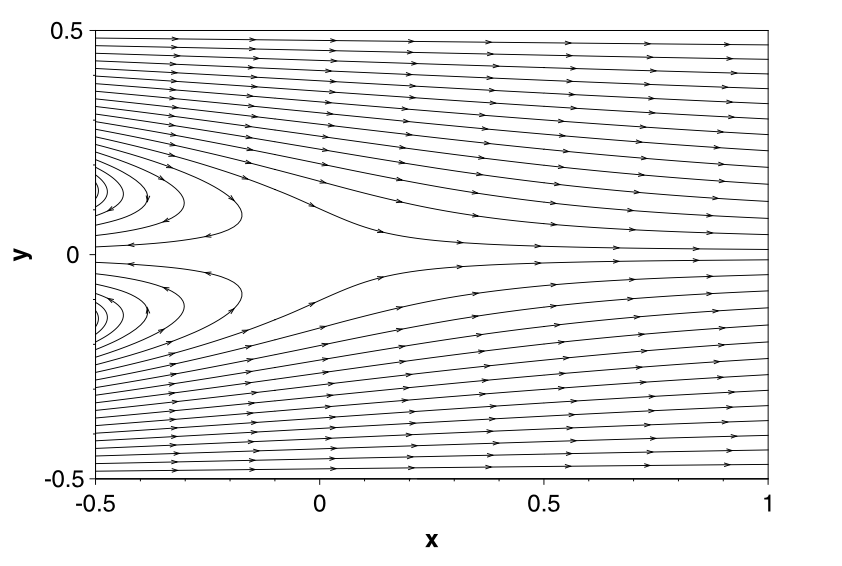
论文中的数值试验主要分如下几点: ##### 空间收敛性
给定\(\Delta t = 0.005\), \(C_0=0.1\), 网格不变,随着谱元的阶数提升,速度误差减小,直到"饱和"。饱和后,误差受到时间步长的影响不再变化。评估误差饱和之前的变化是否满足空间收敛规律。
\(C_0\)对精度的影响
给定\(\Delta t = 0.005\), 谱元的阶数为\(14\), 分别计算 \(C_0=0.1\) 和 \(C_0=500\),比较误差的变化,时间算到了\(10^5s\).
计算\(C_0\in[10^{-4},10^{14}]\),计算达到稳态后的误差。
稳定性
- 考虑谱元阶数10和16,\(C_0=0.01\), \(\Delta t \in[0.001,1.0]\),发现时间步长过大,误差较大,但是数值计算仍然能够保持稳定。如果是半隐格式,步长稍微增大,数值计算就不再稳定,如下图所示。current scheme exhibits a different behavior and produces stable computations even with much larger \(t\) values.
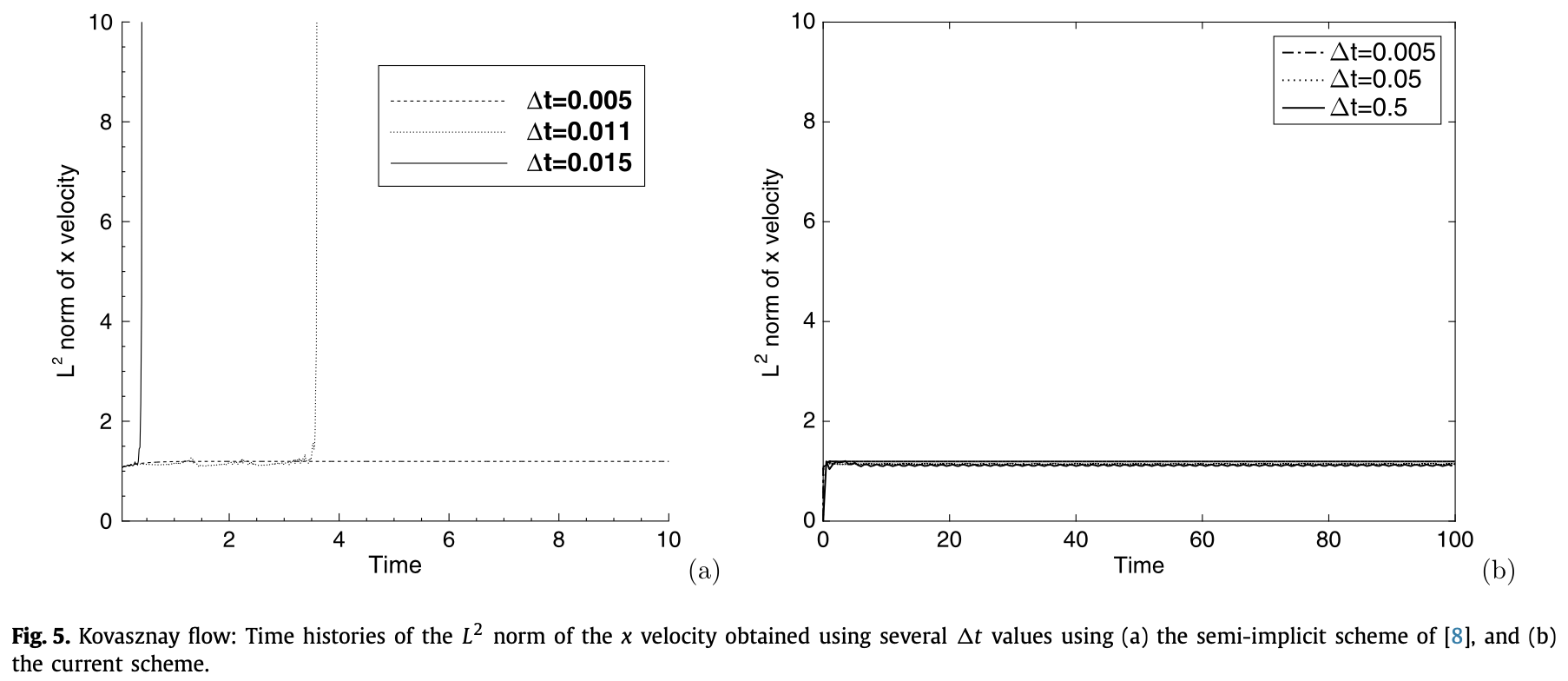
- 时间步长再调大,误差太大,计算结果没有意义了,但是我们的算法还能保持稳定。
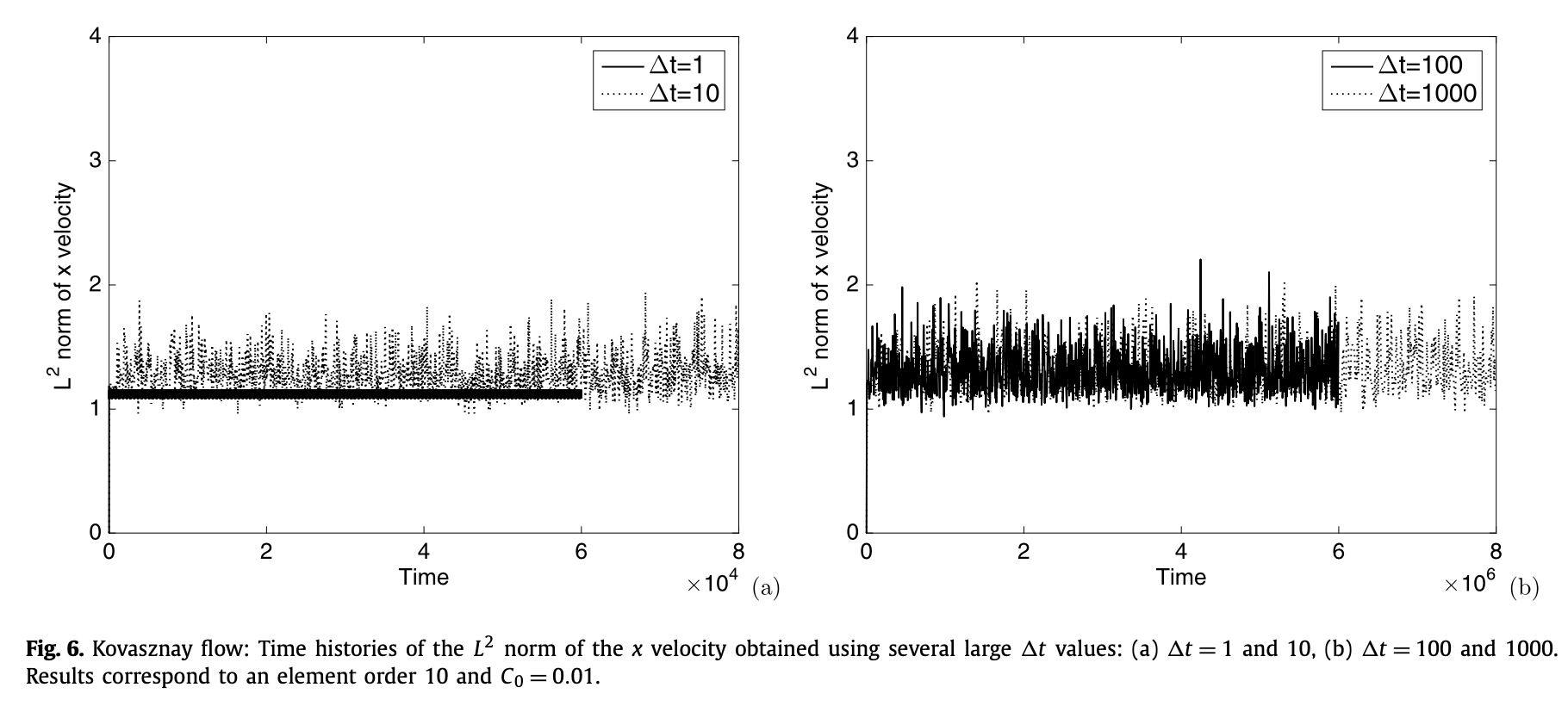
- 画出不同时间步长计算出的\(E(t)\)和\([R(t)]^2\)的曲线,当\(\Delta t\) 很小时,两条曲线几乎相同。随着\(\Delta t\)增加,两条曲线均开始出现波动,差距逐渐增加。这表明,我们提出的数值格式能自动调整\(\frac{R(t)}{\sqrt{E(t)}}\), 显式处理非线性项,因此能使计算更加稳定。
目前,首先是李晓丽的文章中的算例,计算区域为 \(\Omega=(0,1) \times(0,1)\),\(T=1\),\(\nu=1\) , \(\delta=0.1\), \(\Delta t=h=k\). 记 \[ \left\{\begin{array}{l} \left\|e_X\right\|_{\infty, 2}=\max _{0 \leq n \leq m}\left\{\left\|e_X^n\right\|\right\}, \\ \left\|e_p\right\|_{2,2}=\left(\sum_{n=0}^m \Delta t\left\|P^{n+1 / 2}-p^{n+1 / 2}\right\|_{l^2, M}^2\right)^{1 / 2} \\ \left\|e_q\right\|_{\infty}=\max _{0 \leq n \leq m}\left|Q^n-q^n\right|, \end{array}\right. \] 其中, \(X=\mathbf{u}, d_x u_1, D_y u_1\).
算例一
\[ \left\{\begin{array}{l} p(x, y, t)=\exp (t)\left(x^3-1 / 4\right) \\ u_1(x, y, t)=-\exp (t) x^2(x-1)^2 y(y-1)(2 y-1) / 256 \\ u_2(x, y, t)=\exp (t) x(x-1)(2 x-1) y^2(y-1)^2 / 256 \end{array}\right. \]
